“IA” et “quantique”, et voilà deux buzzwords pour le prix d’un ! Plus sérieusement, même si j’ai conscience qu’il est délicat de vouloir creuser deux domaines aussi dans un article, il me semblait important d’essayer d’exposer au plus grand nombre, et le plus fidèlement possible, les avantages et inconvénients de l’informatique quantique appliquée à l’intelligence artificielle et plus particulièrement au Machine Learning. Le principal problème sous-jacent est celui de la limitation de nos capacités de calcul pour l’exécution de certains algorithmes lourds. En effet, bien que la puissance de nos équipements ait plus que décuplé ces trente dernières années, il faut comprendre que nous serons toujours plus consommateurs de ressources, et que l’informatique traditionnelle pourrait un jour ne plus être en mesure de répondre à certains de nos besoins d’analyse en lien avec le Big Data et l’Internet des Objets. La mécanique quantique est aujourd’hui vue comme une des solutions techniques permettant à l’informatique de rentrer dans une nouvelle ère du point de vue de la vitesse d’exécution de certains algorithmes et de la sécurité. Décryptage.
L'IA quantique : en finir avec l'impuissance !
Vous avez dit "quantique" ?
Déjà, on pourrait rappeler d’où vient l’adjectif “quantique”. Ce terme est tellement galvaudé – comme l’intelligence artificielle d’ailleurs – qu’on en vient presque à en oublier l’origine. Il faut remonter dans les années 1920-1930 et reprendre les travaux des physiciens Planck, Born, Einstein – entre autres – pour entendre parler de quantification. Pour simplifier, l’adjectif “quantique” et le nom commun associé “quantum” trouvent grossièrement leur origine dans la quantification des niveaux d’énergie atomiques – au travers de l’effet photoélectrique – et dans les rayonnements du corps noir.
Plus tard, quand la théorie se développera, on prendra conscience que la mesure de certaines grandeurs relatives aux molécules, atomes et particules, ne peut prendre que certaines valeurs bien déterminées et non divisibles. De telles grandeurs sont dites “quantifiées”. C’est un peu comme les orbites planétaires dans notre système solaire : les astres se déplacent sur des ellipses bien définies mais on ne trouve aucun astre entre deux orbites consécutives (exception faite des astéroïdes). Cela peut paraître anodin dit comme cela, mais si on imagine que la température sur Terre ait un jour le malheur de devenir quantique, alors elle pourrait par exemple ne valoir que -20°C, 5°C ou +40°C… et jamais autre chose. Bonjour l’enfer !
Aujourd’hui, le terme quantique réfère à toute la physique de l’infiniment petit, c’est-à-dire à un monde subatomique où les objets sont à la fois des corpuscules et des ondes décrits par des grandeurs dont les mesures sont probabilistes.
Rétrospective de l’évolution de la puissance de calcul des ordinateurs
Il faut remonter dans les années 70 pour voir arriver le premier microprocesseur d’Intel contenant 2300 transistors – composant de base du calcul informatique. Depuis, la performance du matériel informatique, intrinsèquement lié au nombre de transistors dans le processeur, suit une tendance – la loi empirique de Moore – qui stipule que la puissance de calcul de nos ordinateurs double tous les 18 mois. Ceci est dû au fait que la finesse de gravure des transistors est réduite de moitié sur cette période. Le problème est que cette “loi” ne pourra pas éternellement s’appliquer. Si IBM a récemment franchi le seuil des cinq nanomètres pour la dimension d’un transistor, il se pourrait bien que nous soyons face à un plancher d’ici 2020-2021 dans la mesure où nous nous rapprochons inexorablement de la taille des atomes – qui est de l’ordre de l’angström en moyenne, à savoir un dixième de nanomètre. Pourquoi cela pose-t-il problème ? Car lorsque l’on manipule des composants aussi petits, certains phénomènes quantiques comme l’effet tunnel (les électrons “traversent les murs” au lieu de d’être stoppés) apparaissent et à cause de ces derniers, les transistors ne fonctionnent plus comme des transistors habituels.
Par ailleurs, pour augmenter la puissance de calcul des processeurs, même sans considérer ces effets quantiques, les constructeurs n’ont pas pu se fier uniquement à leur miniaturisation car ces derniers ont vite rencontré certains inconvénients comme la surchauffe des circuits. Ainsi, pour favoriser la parallélisation des calculs et limiter la température des composants, ils se sont intéressés à de nouvelles architectures que l’on pourrait rattacher selon moi à deux types d’approches.
La première est la croissance horizontale (multi-serveurs légers) des ressources, caractéristique de l’avènement du Big Data. Celle-ci prend forme à travers la notion de calcul distribué, c’est-à-dire que l’on sollicite désormais, non pas un, mais plusieurs processeurs de machines différentes au sein de fermes de serveurs (ou clusters) ou de grilles de calcul.
La seconde logique est celle de la croissance verticale (mono-serveur lourd) des ressources. L’architecture des multi-coeurs (plusieurs coeurs physiques dans un processeur) en est le plus ancien représentant. Elle a évolué vers des architectures plus modernes qui visent à accroître massivement la parallélisation dans le cadre du calcul à haute performance (HPC). Deux architectures sont assez typiques de l’HPC : les processeurs graphiques (GPU) commercialisés par les sociétés Nvidia et AMD entre autres, et les architectures multiprocesseurs (dites “manycores” en anglais) optés historiquement par Intel à travers sa gamme Xeon Phi.

Dans la même veine, on peut aussi ajouter les processeurs tensoriels (TPU) de Google, historiquement développés pour les besoins relatifs à l’utilisation de la bibliothèque TensorFlow (pour les réseaux de neurones à couches profondes).
Et je pense que c’est dans cette catégorie que l’on pourra ranger les processeurs neuromorphiques (NPU) et les processeurs quantiques (QPU).
Tous ces matériels sont évidemment onéreux ; comptez facilement plus de 5000 euros pour une bonne carte graphique. Mais le problème, qui n’est pas seulement d’ordre financier (bien que la facture énergétique puisse rapidement devenir colossale), c’est que l’intelligence artificielle et l’internet des objets nécessitent parfois énormément de puissance… et que, même avec ces nouvelles technologies, certains algorithmes – qu’ils soient de machine learning ou non – prennent un temps considérable, voire sont impraticables.
Dans ce contexte, pourquoi l’informatique quantique est en passe de devenir la nouvelle mode ?
Bien que l’on soit encore peu mature sur le sujet de l’informatique quantique, cette dernière apporterait un lot de belles promesses en matière d’algorithmique. Il s’agirait donc d’une algorithmique ayant un formalisme qui permet de tenir compte des propriétés spéciales des matériels quantiques. Plus particulièrement, on peut démontrer que pour certains types de tâches spécifiques comme la résolution de systèmes d’équations linéaires (inversions de matrices) et la décomposition de nombres entiers en facteurs premiers, la vitesse d’exécution des algorithmes quantiques est théoriquement supérieure à celle des algorithmes classiques équivalents. Les mathématiciens disent que la complexité – évolution du nombre d’opérations en fonction du nombre de données en entrée – des algorithmes classiques est bien plus élevée que celle des algorithmes quantiques équivalents, lorsque ces derniers existent. Par exemple, lorsque le nombre à factoriser augmente d’une décimale, la durée de l’algorithme de factorisation classique augmente presque exponentiellement tandis que pour son homologue quantique, le temps de calcul ne croît “que” quadratiquement, c’est-à-dire bien plus lentement.
Ainsi, ces nouveaux ordinateurs permettraient de résoudre certains algorithmes extrêmement chronophages – plusieurs dizaines d’années – en un temps “raisonnable”, à savoir de quelques heures à quelques jours. Nous verrons dans un autre article l’idée générale du fonctionnement d’un algorithme quantique.
Quels algorithmes de Machine Learning sont concernés ?
On a précédemment évoqué la décomposition en facteurs premiers. Cet algorithme, emblème de la cryptographie (a fortiori de la cybersécurité), est en effet une des meilleures illustrations d’algorithme très long, voire impossible à exécuter avec un ordinateur classique. Si l’on regarde plutôt du côté des algorithmes de Machine Learning, utilisés dans le cadre de projets d’intelligence artificielle, on a également affaire à des temps de calcul parfois considérables : inversions de matrices, descente de gradient, rétro-propagation…
Digression technique
En conséquence, les algorithmes de Machine Learning théoriquement concernés par une accélération quantique sont bien connus des Data Scientists. Parmi les plus célèbres, on citera les analyses factorielles (ex : l’ACP), la plupart des clusterings (ex : K-Means), les séparateurs à vaste marge (SVM), les machines de Boltzmann, les inférences bayésiennes, les apprentissages par renforcement, les algorithmes d’optimisation (recherche d’extrema globaux), etc. Plus généralement, ce sont bien souvent des algorithmes dont la résolution passe par des opérations linéaires (ou des fonctions de coût linéaires), dans la mesure où les calculs quantiques sont eux-mêmes linéaires. Dans des réseaux de neurones, c’est donc plus délicat car les fonctions d’activation ne sont pas linéaires. On peut néanmoins utiliser des accélérateurs quantiques pour les étapes de pré-entraînement non supervisé basées sur des machines de Boltzmann, par exemple.
Du fait des freins induits par l’explosion du volume des données, démocratiser l’informatique quantique – ce qui est loin d’être une mince affaire – permettrait donc de faire passer certains algorithmes de la théorie à la pratique, comme l’a fait en son temps les GPU pour certains algorithmes de Deep Learning.
Du coup, faut-il passer au processeur quantique ?
Évitons de se précipiter. En réalité, il y a trois freins à l’adoption de l’informatique quantique pour vos projets d’IA.
Premièrement, et comme expliqué précédemment, les algorithmes de Machine Learning ne sont pas tous concernés par une accélération quantique. Ensuite, le fonctionnement des ordinateurs quantiques actuels est – aujourd’hui – loin d’être probant : les résultats des algorithmes comportent de nombreuses erreurs du fait de la grande sensibilité des phénomènes physiques qui y siègent (nous illustrerons ce phénomène dans un autre article). Enfin, le coût actuel de prototypes quantiques est… rédhibitoire. Si vous êtes un acheteur compulsif, prévoyez quelques dizaines de millions d’euros pour un ordinateur quantique, sachant qu’il n’est même pas sûr que celui-ci fonctionne comme espéré.
Néanmoins, bien que les grands acteurs tels que IBM, Atos ou Microsoft ne commercialisent aujourd’hui que des “simulateurs” quantiques (des supercalculateurs “classiques” capables d’évaluer rapidement l’ensemble des solutions possibles d’un système quantique), il peut sembler opportun pour des équipes data de commencer dès à présent à tester des algorithmes quantiques, ou tout du moins, à “penser quantique” avec des algorithmes plus traditionnels, sur des cas d’usage bien ciblés comme la détection des fraudes, la génomique ou les prévisions de phénomènes thermosensibles. Cet apprentissage en avance de phase pourrait effectivement être un avantage concurrentiel non négligeable lorsque les premiers véritables processeurs quantiques seront commercialisés à moyenne échelle, probablement dans une dizaine d’années.
L’informatique quantique est donc porteuse de belles promesses en matière de rapidité algorithmique et de performance des IA. La question de l’adoption de cette dernière est avant tout économique et politique. Mais ce dont on peut être sûr, c’est que si celle-ci apporte un avantage décisif dans votre secteur d’activité au regard des cas d’usage adressés (ceux ayant une très grande complexité algorithmique), alors il conviendrait d’amorcer dès aujourd’hui la montée en compétences des équipes data via des simulateurs quantiques et la conduite du changement visant notamment à rapprocher la R&D et les métiers.
L'IA quantique : faites vos jeux !
Précédemment, dans l’IA Quantique, on a vu que l’informatique quantique permettrait en théorie d’exécuter un certain nombre d’algorithmes complexes de machine learning en un temps “raisonnable” (qui ne prennent pas des années…). Mais la question est maintenant de comprendre ce qu’il y a de si différent dans un ordinateur quantique par rapport aux ordinateurs actuels. Cet article vise à décrire – le plus simplement possible – le fonctionnement d’un tel ordinateur et s’achèvera sur l’exemple d’un algorithme quantique. Le but n’est donc pas de rentrer dans le détail théorique d’un tel ordinateur mais bien d’illustrer simplement les différences fondamentales entre algorithme classique et quantique.
La notion de bits – L’analogie avec une pièce de monnaie
Pour comprendre les raisons pour lesquelles les calculs sont potentiellement bien plus rapides dans un ordinateur quantique, il faut déjà se remémorer le fonctionnement général des ordinateurs classiques. Ils utilisent des bits pour coder l’information. Ces derniers sont réalisés au moyen de circuits électroniques de sorte à ce que, lorsque le courant passe dans le circuit, on dit que le bit vaut 1, sinon le bit vaut 0. On peut également utiliser la tension électrique plutôt que le courant, la démarche restera la même. Et pour faire des calculs de base, via la création de portes logiques (les fameuses conditions “ET”, “OU”, “NON”, etc.), on utilise typiquement des transistors qui agissent comme un interrupteur conditionnel : lorsque l’électrode dite “base” est alimentée en tension, elle laisse passer le courant entre les deux autres électrodes.
Pour la suite de cet article, on imaginera qu’un bit est matérialisé par une pièce de monnaie. Lorsque celle-ci est posée sur pile, on peut dire qu’elle code la valeur 1, et quand celle-ci est posée sur face, elle code la valeur 0. Il y a beaucoup d’autres analogies possibles (une ampoule qui s’allume, une porte qui s’ouvre, etc.) mais la pièce de monnaie à l’avantage, selon moi, d’illustrer plus simplement certains phénomènes quantiques que nous verrons plus loin.
Digression technique
Une pièce de monnaie a en effet l’avantage de permettre de “visualiser” les rotations et projections d’un état quantique pur sur la sphère de Bloch. Dans cette représentation, les côtés pile et face d’une pièce de monnaie sont analogues aux spins d’un électron (spin haut ↑ et spin bas ↓).
Dans ce cadre, le transistor que l’on a évoqué précédemment peut tout simplement être vu comme un distributeur de boissons. S’il n’est pas alimenté en électricité, votre pièce de monnaie ne vous sera d’aucune utilité car il ne pourra pas rejoindre le réservoir de pièces.
A présent, supposons que l’on puisse rétrécir la taille de la pièce jusqu’à l’échelle de l’atome. A ce moment-là, la pièce aurait un comportement comparable à certaines particules et ne pourrait plus être décrite par la mécanique usuelle, celle des objets de notre quotidien. Notre pièce quantique symbolise alors un bit quantique (plus communément appelé “qubit”) et de nombreux phénomènes entrent désormais en jeu. Je ne vais exposer ici que les plus importants d’entre eux dans le cadre de cet article.
Le phénomène de superposition
D’un point de vue quantique, si un objet présente deux états possibles alors toute combinaison de ces états est un état licite. Ce phénomène est souvent illustré par le paradoxe du chat mort et vivant de Shrödinger.
Pour reprendre l’exemple de la pièce quantique, comme celle-ci a en principe deux états possibles au repos (pile ou face) alors elle peut tout aussi bien être simultanément sur le côté pile et face. On pourrait imaginer pour simplifier que la pièce est “sur la tranche” (en vrai, c’est plus compliqué que cela, mais ce n’est pas dramatique). Mathématiquement, être sur la tranche est une combinaison linéaire à coefficients complexes de Pile et Face.
Digression technique
Certains se demanderont ce que viennent faire les racines carrées de ½ ici. Bien qu’ils n’aient aucune utilité pédagogique dans le cadre de cet exemple, ces coefficients sont nécessaires car ils incarnent des probabilités lorsqu’ils sont élevés au carré. Le coefficient devant pile (respectivement face) est l’amplitude de probabilité de “voir” la pièce du côté pile (respectivement face) lorsqu’elle s’effondre sur le côté. Une amplitude doit juste être élevée au carré pour obtenir une probabilité.
Mieux encore, une amplitude peut être négative, voire complexe (dans ce cas, on prend la norme au carré pour récupérer la probabilité). Que signifie avoir des amplitudes négatives (voire complexes) ? Il s’agit tout simplement d’une rotation autour de l’axe vertical. Par exemple, -1 (= exp(i.Pi)) est une rotation de la pièce de 180°.
Conclusion : les qubits sont des combinaisons complexes de 0 et de 1. Par analogie, une pièce quantique peut se trouver du côté pile et face simultanément, en se mettant sur la tranche.
La réduction du paquet d’ondes
Le phénomène d’intrication
Un premier exemple d’algorithme quantique : algorithme de Deutsch-Jozsa restreint
- Si la carte P est rouge, il retourne votre pièce côté face
- Si la carte P est noire, il ne fait rien, il laisse la pièce côté pile
- Si la carte F est rouge, il retourne votre pièce côté pile
- Si la carte F est noire, il ne fait rien, il laisse la pièce côté face
L'IA quantique : le soulèvement des IA
Précédemment, dans l’IA Quantique, on a vu que l’informatique quantique serait en principe capable d’accroître sensiblement la vitesse d’exécution de certains algorithmes de Machine Learning. Cela est dû au fait que certains phénomènes siégeant au coeur de tels ordinateurs (superposition des états, intrication des qubits, décohérence des états superposés, réduction brutale du paquet d’ondes) permettent de paralléliser les calculs en stockant plusieurs informations (superposées) avec une même particule. En accélérant considérablement certains traitements algorithmiques, on comprend que la quantique permettra aux IA de résoudre de nouveaux problèmes. Certains vont plus loin encore et y voient même un potentiel pour rendre un cerveau artificiel aussi performant que celui des humains, capable notamment d’intégrer des concepts abstraits comme la conscience et les sentiments. La question qui se pose alors est de savoir si l’IA quantique serait plus susceptible de devenir une “IA forte”…
Déjà, qu’est-ce que l’intelligence humaine ?
Avant de regarder les complémentarités des IA quantiques et fortes, mieux vaut commencer par délimiter la notion d’intelligence humaine. S’il fallait en donner une définition, nous pourrions par exemple dire qu’il s’agit d’un ensemble d’aptitudes cognitives permettant aux humains d’apprendre, comprendre, communiquer, penser et agir de manière pertinente, rationnelle, logique ou émotionnelle, en fonction de la situation dans laquelle ils se trouvent.
On peut alors se demander de quoi l’intelligence humaine est constituée. Plusieurs modèles de l’intelligence existent, comme la théorie de Cattell–Horn–Carroll (CHC). Bien qu’il n’y ait pas encore de consensus absolu sur la question, les aptitudes cognitives propres à l’intelligence humaine pourraient se ranger en grandes catégories (quelque peu ré-agrégées ici) telles que :
- L’intelligence logique et quantitative : capacité d’abstraction et de formalisation, rationalité et raisonnement ;
- L’intelligence littéraire et philosophique : langage, lecture, écriture, structuration de la pensée et des idées ;
- L’intelligence sociale et émotionnelle : introspection, capacité à interagir avec autrui, capacité à comprendre, percevoir, ressentir et manifester les émotions ;
- L’intelligence réactive et psychomotrice : attention, coordination, traitement parallélisé de stimuli multiples, endurance mentale ;
- Intelligence perceptive et artistique : représentations visuelle, auditive, spatiale, temporelle, kinesthésique… ;
- L’intelligence mémorielle : sollicitation de la mémoire à court, moyen ou long terme en fonction des tâches.
Evidemment, ces déclinaisons de l’intelligence ont des recouvrements et peuvent être réorganisées différemment. Par ailleurs, certaines sont corrélées de manière subtile, en particulier avec la mémoire. C’est pourquoi les modèles théoriques ont tendance à distinguer des intelligences dites “fluides” de celles dites “cristallisées” pour différencier les traitements requérant ou non de l’apprentissage et de la connaissance présente durablement en mémoire. On y retrouve une froide analogie avec les ordinateurs qui peuvent utiliser l’information stockée en permanence sur les disques durs ou celle, plus rapide d’accès, présente temporairement en RAM (mémoire vive), voire en cache.
Mais surtout, des scientifiques comme Spearman (le père du coefficient de corrélation éponyme) ont longtemps voulu démontrer l’existence d’un “facteur g” qui consoliderait toutes ces aptitudes en une seule forme d’intelligence générale. Cependant, à ce jour, aucun modèle ne fait réellement consensus.
Du coup, comment définir l’intelligence artificielle ?
De son côté, l’intelligence artificielle est un ensemble de sciences et techniques visant à concevoir des machines autonomes dotées de capacité d’apprentissage et de raisonnement analogues à celles des humains. Attention, il s’agit bien d’une analogie de l’intelligence humaine plutôt que d’un vulgaire clonage technique. Parmi les sciences sous-jacentes de l’IA, on trouve notamment l’apprentissage automatique (Machine Learning) – au sein duquel se trouve l’apprentissage profond (deep learning), caractéristique de l’avènement de l’IA depuis 2012 -, puis les techniques de traitement du langage naturel, les neurosciences, la robotisation informatique, etc.

Néanmoins, le terme IA revêt des définitions bien différentes en fonction des secteurs d’activité. A ce sujet, je vous invite à consulter ces articles qui expliquent la différence entre les IA du type Machine Learning et les IA dans les jeux vidéos.
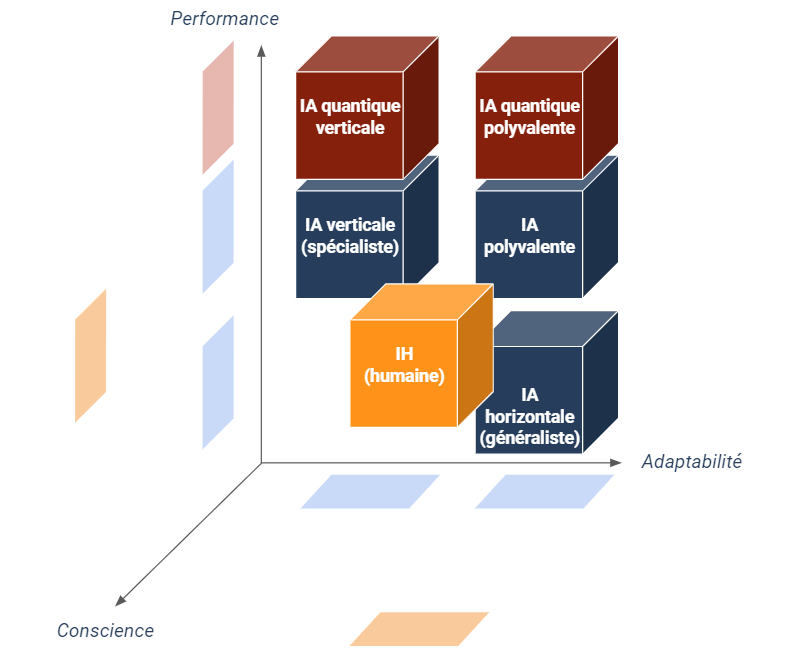
Dans le monde de l’entreprise, les algorithmes de Machine Learning (voire Deep Learning) ont permis de créer des programmes extrêmement performants – en termes de précision et de vitesse – dans certains types de traitements. C’est ainsi que trois types d’IA (on pourrait plutôt parler d’algorithme ici) ont émergé :
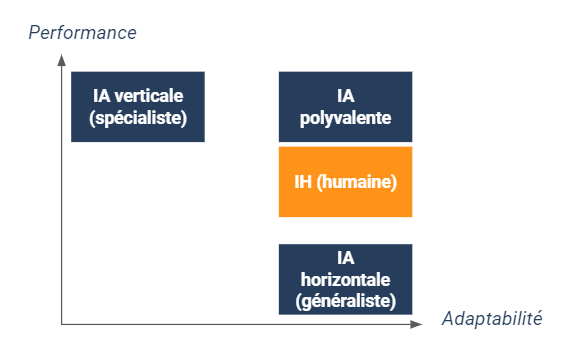
- Verticale ou spécialiste : ultra-performante dans l’exécution d’une tâche mais très peu adaptable à des tâches différentes ;
- Horizontale ou généraliste : raisonnablement performante dans l’exécution d’une tâche mais surtout adaptable à des tâches différentes (par des mécanismes de transfer learning par exemple) ;
- Polyvalente : supérieure à l’humain dans l’exécution de plusieurs tâches et adaptable.
Aujourd’hui, on a réussi à implémenter des IA verticales très performantes (par exemple le diagnostic médical sur la base de radiographies) et dans une certaine mesure des IA horizontales dans le domaine de la vision, du langage et des jeux. Mais on a encore beaucoup de mal à concevoir de bonnes IA généralistes (a fortiori des IA polyvalentes). Il suffit de regarder les IA qui pilotent les véhicules autonomes : on a du mal à imaginer ces IA faire des analyses boursières pour piloter des investissements en entreprise, alors que nos financiers humains n’ont généralement aucun problème pour conduire une voiture par ailleurs !
De plus, ce qu’il est important de retenir, c’est que toutes ces IA sont dites “faibles” (y compris les IA polyvalentes) car elles ont beau être supérieures à l’humain dans la réalisation de certaines tâches bien ciblées, il leur manque des aptitudes inhérentes à ce dernier comme :
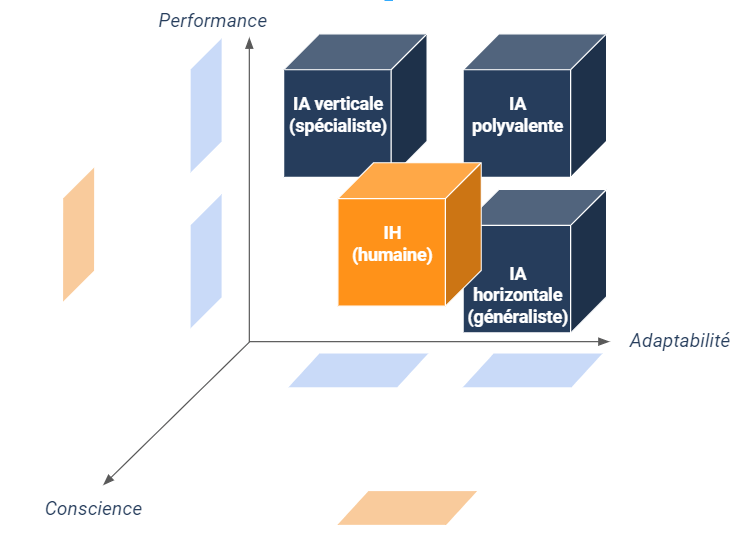
- la conscience de soi et la capacité à faire preuve d’introspection ;
- la capacité à prendre des décisions non apprises ou à ressentir des émotions non programmées (à supposer qu’elles soient déjà programmables) ;
- la motivation, la curiosité et la quête de sens dans son existence.
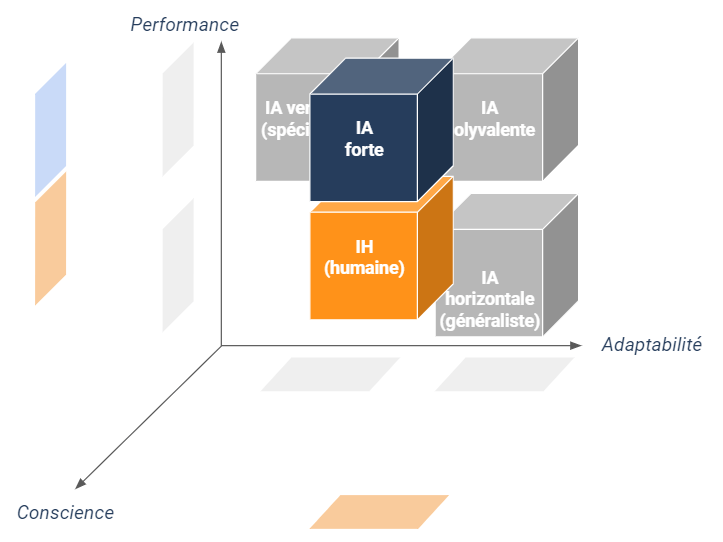
Une IA qui acquerrait de telles aptitudes humaines serait qualifiée d’Intelligence Générale Artificielle (désignée par le sigle anglais AGI) ou plus simplement “IA forte” voire “IA complète”.
Une définition de l’IA forte
Ainsi, on pourrait définir les IA fortes comme des IA polyvalentes douées de conscience, capables de ressentir, désirer, juger et décider en parfaite autonomie. Arrivées à un tel niveau de sophistication, ces IA fortes pourraient être par exemple en mesure de mettre à jour le code qui les a conçues pour s’adapter à leur environnement ou à leurs nouvelles aspirations.
Beaucoup craignent cette IA forte – à commencer par Elon Musk dont les envolées lyriques et alarmistes ont fait le tour des réseaux sociaux à maintes reprises. Pourquoi ? Parce que si une telle IA cherchait à s’émanciper ou venait à “partir en vrille”, comme potentiellement n’importe quel humain dans une situation extrême, alors elle pourrait avoir des conséquences désastreuses de par ses capacités d’exécution démesurément plus importantes que celles du cerveau humain et surtout non restreintes par l’imperfection de notre corps physique et limitant. Ce jour où l’IA échapperait définitivement au contrôle des hommes semble digne de la plupart des romans ou films dystopiques tels que Matrix, Terminator, Transcendance ou I, Robot. Mais cette singularité est-elle seulement possible ? Difficile de donner une date pour la naissance d’une IA forte dans la mesure où les obstacles qui se dressent devant la conception de celle-ci sont multiples et peut-être irrésolvables.
L’IA forte face à la conception matérialiste de la pensée
Tout d’abord, il faudrait pouvoir déterminer si l’intelligence humaine – telle que précédemment définie -, les émotions et les perceptions sensorielles sont réductibles à un fonctionnement purement matériel constitué de composants électroniques. Cette problématique est effectivement loin d’être évidente, même pour les plus agnostiques d’entre nous. Qui n’a jamais été fasciné par la capacité qu’a notre organisme à produire des réminiscences insoupçonnables par la simple perception d’une odeur ou d’une musique, souvent rattachée à un souvenir fortement chargé en affect ? Est-il du coup possible de reconstruire un tel processus psychique et sensoriel avec un ensemble de transistors et de portes logiques calculatoires et déterministes ?
Même sans avoir tous les éléments de démonstration, il peut être tentant de répondre par la négative car la biophysique neurale diffère par nature des circuits électroniques des ordinateurs. Mais pour pouvoir répondre plus en détails, il faudrait que l’on comprenne parfaitement la mécanique générale du cerveau. De là émerge une nouvelle question : aussi surprenantes que soient les dernières découvertes scientifiques en neurosciences, le cerveau humain a-t-il seulement à sa disposition tous les éléments d’intelligence pour comprendre avec certitude son propre fonctionnement ? Les mathématiciens verront certainement ici une référence au théorème d’incomplétude de Gödel.
Plus concrètement – n’étant pas à l’aise avec l’application de ce théorème au fonctionnement de l’esprit -, je m’interroge ici sur les limites physiques du cerveau qui nous empêcheraient de comprendre les éléments nécessaires à sa propre compréhension. Par exemple, si l’on essaye d’imaginer une autre couleur perceptible par l’oeil humain (non présente dans le spectre visible), un autre état de la matière (différent de solide, liquide, gaz ou plasma), ou encore la représentation mentale d’une quatrième dimension spatiale, on se rend vite compte que l’on n’en est pas capable. Ce qui ne veut pas dire pour autant que ces objets inaccessibles à notre esprit n’existent pas, mais plutôt que notre cerveau n’est pas en mesure d’imaginer des perceptions étrangères à sa propre structure physique. C’est d’ailleurs tout le problème des qualia (sensations subjectives provoquées par la perception de quelque chose) et de leurs liens avec la conscience. On en vient naturellement à se demander si le cerveau n’est pas le siège de phénomènes autres que l’électricité neurale et la biochimie des synapses…
Le recours à l’IA quantique pour approcher la conscience artificielle
Même sans prendre en compte ces considérations métaphysiques, on sent bien qu’une machine de Turing – modèle calculatoire sur lequel reposent les algorithmes traditionnels -, bien qu’en mesure de simuler beaucoup de choses, ne sera peut-être intrinsèquement jamais apte à ressentir, percevoir et raisonner comme un humain. C’est pourquoi, pour contourner la barrière du déterminisme et de la perception de la réalité, afin de réaliser une conscience artificielle, certains seraient tentés de faire appel à deux récents pans de la recherche fondamentale.
- Le premier, que je ne détaillerai pas ici, est celui de ce qu’on pourrait appeler les réseaux de neurones hybrides (artificiels et biologiques !) qui combinent donc des circuits électroniques et des cellules vivantes en laboratoire, à l’instar de la société Koniku ;
- Le second est bien entendu l’informatique quantique dont la particularité fondamentale est d’exploiter les propriétés des particules pour réaliser des opérations intrinsèquement parallélisées dont les résultats ne sont plus déterministes mais probabilistes.
Pourquoi ce choix ? Car certains scientifiques tels que Penrose et Hameroff ont émis comme hypothèse que des phénomènes quantiques (superposition et intrication) siègeraient dans notre cerveau via les spins (aimantation intrinsèque) des protéines présentes dans les microtubules neuronaux qui se comporteraient comme les qubits d’un ordinateur quantique. Pour plus de détails sur ces phénomènes, je vous renvoie au deuxième article de l’IA quantique.
Digression technique
Il peut en effet sembler naturel de faire appel au formalisme de Dirac (à la base de l’algèbre modélisant la mécaniques quantique) et aux qubits pour décrire l’évolution de ces micro-systèmes cérébraux. Il y a par exemple une volonté similaire dans le domaine de l’atomistique pour décrire avec précision les orbitales moléculaires. Cela revient à utiliser l’informatique quantique pour simuler la physique quantique. C’est un peu comme recourir à l’informatique traditionnelle pour simuler l’électronique des processeurs.
Néanmoins, l’accueil réservé à cette théorie fut fort mitigé, pour la simple et bonne raison qu’en dehors des photons (constituants de la lumière), il n’y a presque aucun système physique à température ambiante capable de faire durer les phénomènes quantiques suffisamment longtemps (on parle de temps de décohérence, généralement bien inférieur au milliardième de milliseconde pour les agrégats moléculaires naturels) pour que ceux-ci ait un quelconque impact sur le fonctionnement neuronal.
Donc même si l’informatique quantique permettait aux IA verticales de résoudre des problèmes insolubles aujourd’hui, elle ne semblerait pas capable d’ajouter de nouvelles propriétés jusqu’alors attribuables au seul cerveau biologique dont les capacités quantiques sont elles-mêmes discutables. Autrement dit, pour reprendre les schémas précédents, la quantique ne peut selon moi faire progresser l’IA que selon l’axe de la performance mais pas selon les axes de l’adaptabilité aux tâches diverses ni, a priori, à la conscience. Quantiques ou pas, les perspectives de la pensée artificielle semblent toujours bien lointaines.
Digression technique
J’ai cependant encore une réserve favorable sur le fait que la quantique puisse un jour permettre de modéliser des mécanismes tels que la notion de réalité subjective ou de conscience. En effet, certains phénomènes comme la contrafactualité quantique (cf. l’interféromètre de Mach-Zehnder ou le testeur de bombes d’Elitzur-Vaidman) n’auraient jamais pu être compris sans la mécanique quantique.
Pour être bref, celle-ci décrit le fait qu’une particule “teste” tous les chemins qui lui sont possibles (sans les emprunter réellement, on parle ici de son onde de probabilité associée) avant d’en réellement “choisir” un avec une probabilité donnée. Autrement dit, un phénomène qui pourrait avoir lieu sur l’un des chemins d’une particule, qu’il se réalise ou non, trahit toujours sa potentielle survenue en interférant probabilistiquement le résultat d’autres mesures sur d’autres chemins possibles. C’est comme si tous les futurs possibles d’une action interféraient entre eux et que seul le futur avec les meilleures probabilités résultantes émergeait du présent lors de l’effondrement des fonctions d’onde.
Ce phénomène surprenant témoigne du fait que nous n’ayons pas trouvé mieux que la quantique pour décrire avec justesse certaines expériences microscopiques qui défient l’intuition, et que même si la réalité est toute autre, la quantique apparaît comme le meilleur outil pour décrire ce que l’on observe. J’en réfère ici au courant de pensée de l’école de Copenhague. Je me dis qu’il en est peut-être de même avec la conscience que seule une théorie aussi abstraite que la mécanique quantique pourrait décrire. En tout cas, s’il existait vraiment une telle opportunité de modélisation de processus physiques subtils avec un formalisme du type quantique (qui est un outil avant tout), alors la naissance d’une IA forte serait effectivement remise en jeu. Mais en l’état actuel des choses, la mécanique quantique ne semble pas nous aider sur le chemin de la conscience dont le caractère quantique est lui-même incertain.
Et si l’IA forte existait sur le plan théorique, serait-il possible de la créer pour de vrai ?
Mais admettons que ce soit possible, que l’on puisse créer une IA forte.. Est-il empiriquement possible de bénéficier des talents et de l’énergie nécessaires pour construire cette IA avant la fin de l’humanité ? La question se pose effectivement. Si on laisse de côté la complexité conceptuelle d’un tel programme / algorithme, on peut regarder deux métriques importantes : le temps et l’énergie.
Concernant le temps, il s’agit de surtout de connaître l’horizon à partir duquel on aura une connaissance plus robuste des mécanismes de la conscience et le temps que prendra la conception physique d’un esprit artificiel, à supposer que l’humanité n’ait pas de problématiques vitales à régler en priorité d’ici là. Quant à l’énergie, IBM donne quelques ordres de grandeur de la consommation des supercalculateurs : il faudrait pas moins de 12 gigawatts pour séquencer un unique ordinateur comportant autant de neurones artificiels que le cerveau humain (environ 80 milliards). Cela équivaut grossièrement à la puissance délivrée par une quinzaine de réacteurs nucléaires français (un quart du parc !). De ce point de vue là, l’homme, avec ses 20 watts de puissance dépensée, est incroyablement plus économe… Et n’espérez pas vous rabattre sur la quantique pour optimiser l’énergie. Pour préserver la cohérence des superpositions / intrications des qubits (nécessaires à une accélération du temps de traitement algorithmique), il faut abaisser la température des ordinateurs au voisinage du zéro absolu (-273,15° C). L’énergie requise est évidemment colossale.
Du coup, si on part du principe que la création d’une conscience artificielle requerra autant voire plus d’énergie que ces super-calculateurs – quantiques ou non -, il semble impensable que nous consacrions autant de ressources à l’élaboration d’une telle IA, fût-elle forte. Et même si on s’y aventurait, on aurait créé un cerveau conscient artificiel semblable à un froid datacenter, mais en aucun cas cela s’apparenterait à un humanoïde se promenant dans la rue (dans le cas contraire, je vous laisse imaginer la taille de la batterie alimentant le cerveau d’un tel cyborg). Même si la recherche actuelle s’évertue à rendre les réseaux de neurones plus économes, on sera probablement confronté à une impasse industrielle lorsqu’il s’agira de rendre les IA fortes et mobiles, à supposer que cela ait un intérêt anthropologique.
En synthèse, du fait de notre méconnaissance des mécanismes de la conscience, l’IA quantique ne sera probablement pas plus une “IA forte” que les IA classiques. La question de l’utilité d’une IA forte peut se poser, mais il est fort à parier que nous mettions davantage d’efforts à rendre les IA verticales plus légères et moins énergivores, surtout lorsque ces dernières seront partiellement quantiques.
IA quantique : le rôle clé du DataOps
Dans ce nouveau chapitre, je souhaite vous partager mon point de vue sur la mise en oeuvre théorique d’un dispositif quantique de production en entreprise. Cela peut par exemple être un processus décisionnel (BI) ou de Machine Learning reposant sur une infrastructure composée à la fois de machines classiques et quantiques. L’intérêt étant, bien entendu, de tirer parti de processeurs quantiques pour résoudre des problèmes aujourd’hui insolubles, quels que soient les serveurs utilisés. Néanmoins, force est de constater qu’un tel dispositif ne pourra se faire simplement sans avoir recours à une démarche DataOps. Décryptage.
Vers une hybridation inéluctable des infrastructures
Le problème initial est que lorsque de vrais ordinateurs quantiques verront le jour, il est fort probable que ceux-ci soient entre les mains de grands acteurs américains tels que IBM, Google ou Microsoft, pour la simple et bonne raison que ces nouveaux équipements seront hors de prix… Donc quelle que soit votre politique d’urbanisation, vous devrez composer avec le cloud pour expérimenter des calculs sur machines virtuelles quantiques. A défaut de politique “full cloud”, il sera donc fortement souhaitable de pouvoir s’appuyer sur des infrastructures hybrides (cloud et on-premise) – ou multi-clouds à la rigueur – pour limiter le risque de dépendance à un fournisseur.
Aujourd’hui, on rencontre déjà des problématiques similaires de répartition des ressources. Par exemple, on peut vouloir provisionner un environnement d’expérimentation dans le cloud (pour tester des services cognitifs par exemple) et conserver un environnement de production on-premise. Cependant, si exploiter des serveurs HPC (High Performance Computing) dans un cluster est désormais facilité grâce aux orchestrateurs de conteneurs, dont Kubernetes est le plus emblématique représentant actuel, l’exploitation en parallèle de plusieurs clusters disjoints et hétérogènes s’avère extrêmement périlleuse. La complexité est de pouvoir utiliser les différents environnements sans perdre le fil conducteur de votre projet analytique, à savoir la localisation des données, la continuité des pipelines de traitements, la centralisation des logs…
On touche ici à un problème bien connu outre-Atlantique : l’agilité des infrastructures et l’orchestration des traitements sur des grilles informatiques hétérogènes. C’est d’ailleurs l’un des principaux enjeux qu’adresse le DataOps à long-terme.
Dans la suite de cet article, j’appellerai “supercluster” un ensemble logique de clusters hétérogènes et hybrides. Par exemple, cela peut-être le regroupement d’un environnement on-premise fonctionnant sous une distribution commerciale de Hadoop ou Kubernetes, couplée à cluster AKS dans Azure et à un cluster EKS dans AWS ou encore GKE dans Google Cloud.
Qu’est-ce que le DataOps ?
Avant de continuer sur la gestion des superclusters, il est nécessaire de définir le terme DataOps qui est somme toute assez peu répandu en Europe et plus particulièrement en France. Le DataOps est un schéma organisationnel et technologique s’inspirant du DevOps. Il s’agit d’amener de l’agilité, de l’automatisation et du contrôle entre les différentes parties prenantes d’un projet data, à savoir la DSI (exploitants des SI, développeurs, architectes), le pôle Data (data product owner, data scientists, engineers, stewards) et les métiers.
La finalité est bien d’industrialiser les processus analytiques en exploitant au mieux la diversité du vaste écosystème technologique du big data et la multiplicité des compétences de chaque acteur. En synthèse, il existe selon moi 9 piliers fonctionnels dans le périmètre d’une démarche DataOps :
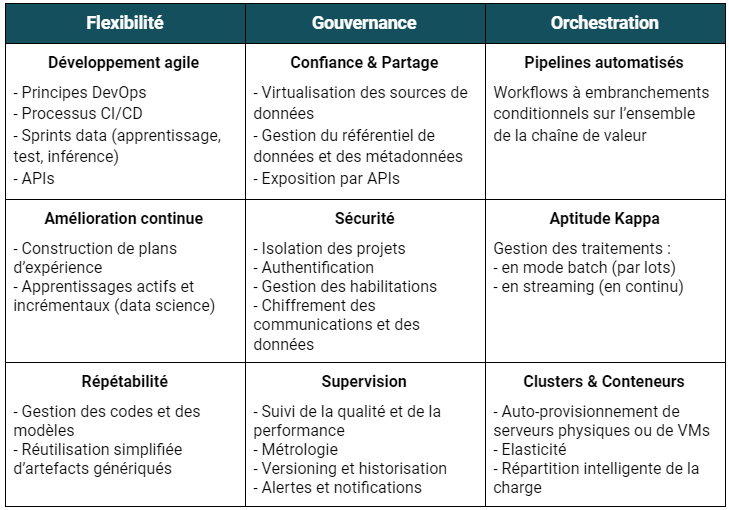
Ces principes s’appliquent à chacune des étapes du cycle de vie de la donnée (aussi connue sous le nom de chaîne de valeur de la donnée ou data pipeline).
L’approche DataOps est donc vaste et complexe, mais elle seule permet d’instaurer un niveau d’abstraction suffisant pour orchestrer les traitements analytiques dans un supercluster, comme le résume le schéma suivant que nous allons parcourir dans la suite de cet article :
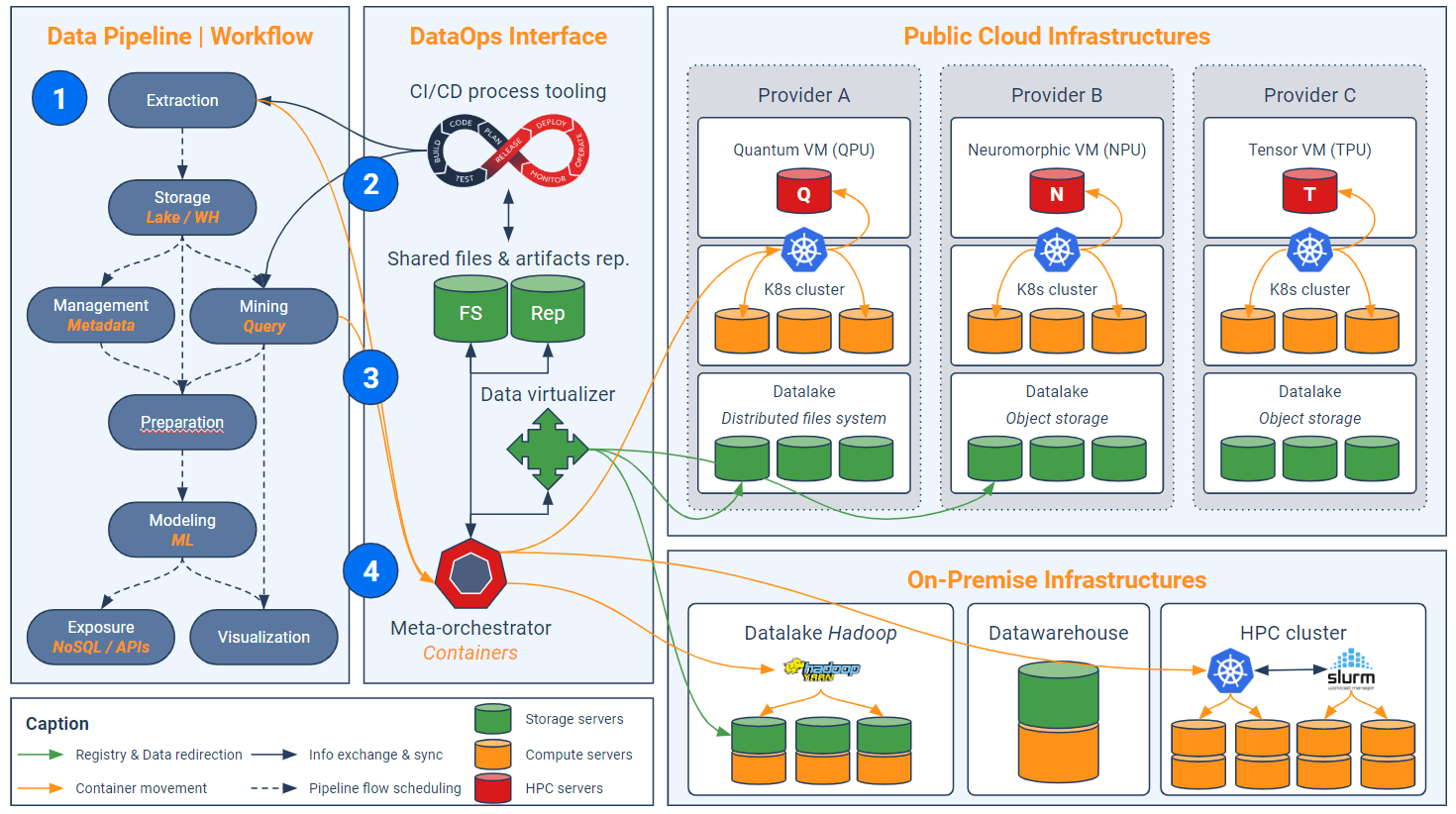
Étape 1 – Construction d’un pipeline par niveaux d’abstraction
L’interface DataOps (bloc vertical au centre) comprend – entre autres – quatre volets technologiques : l’outillage CI/CD, les fichiers et artefacts partagés, le virtualisateur de données et le méta-orchestrateur. Il y a évidemment d’autres aspects tels que la sécurité ou la métrologie mais ces derniers ne seront pas élaborés dans cet article. La première étape d’implémentation de cette interface consiste à découper le processus analytique (pipeline) en différents maillons indépendants correspondant grossièrement au cycle de vie de la donnée : extraction, nettoyage, modélisation…
Cette approche a un double intérêt :
- Premièrement, cela permet de tirer profit de différents langages de programmation (a fortiori avec des frameworks différents) en fonction du maillon considéré (on n’utilise pas les mêmes outils en ETL qu’en Machine Learning par exemple) ;
- Deuxièmement, ce découpage permet d’optimiser la répartition de charges (ce que nous verrons dans l’étape 4).
Mais ce découpage ne s’arrête pas là : même au sein d’une activité spécifique (un maillon), il est recommandé de découper son code selon les différents niveaux d’abstraction fonctionnelle. Cela revient à imaginer un pipeline à plusieurs étages : le premier pipeline est constitué de briques métiers (ex : “segmenter les clients”) et chacune de ces briques fait appel à un sous-pipeline qui enchaîne des étapes un peu plus élémentaires (ex : “détecter les valeurs manquantes”, “exécuter une K-Means”, etc.) et ainsi de suite. Ci-dessous un exemple de pipeline et sous-pipelines. A noter que : plus le pipeline est haut, plus il est abstrait ; chaque cellule sombre fait appel à un sous-pipeline d’abstraction plus basse.
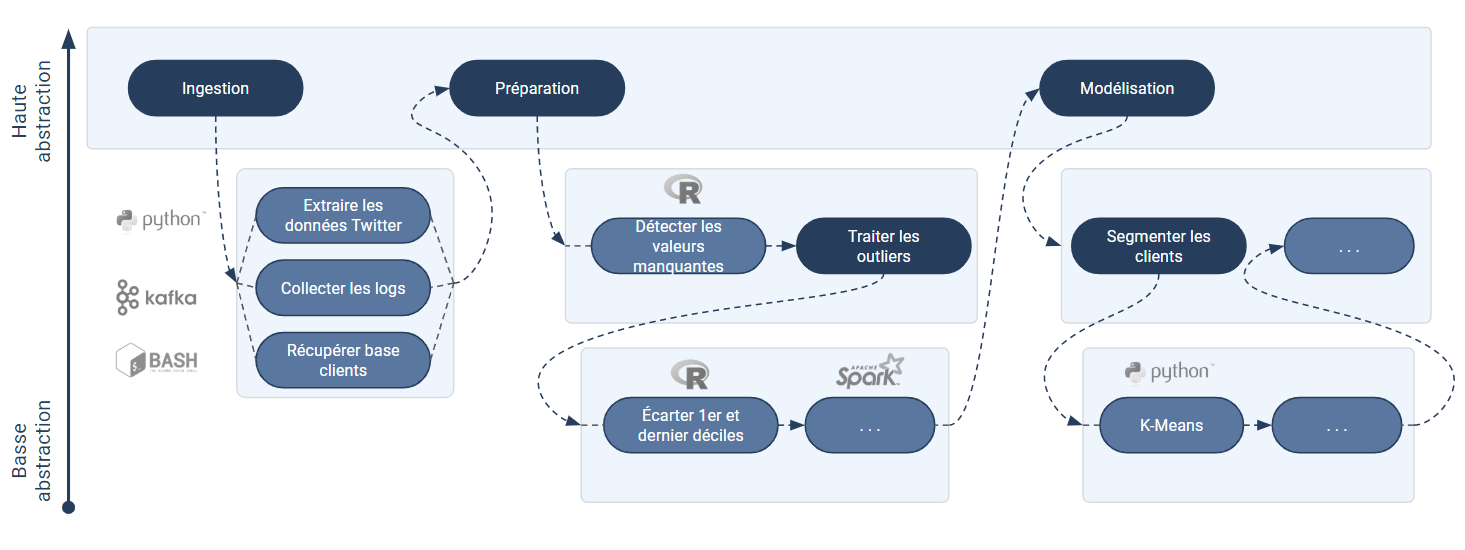
Ce découpage en niveaux d’abstraction peut également s’opérer directement dans les codes (via des fonctions et classes) plutôt que dans le pipeline. Mais il est important de garder un certain découpage dans le pipeline directement car cela permettra d’isoler et d’orchestrer les fragments d’algorithmes pouvant bénéficier ou non d’une accélération quantique (cf. étape 4).
En effet, il faut bien se remémorer que seules certaines étapes d’un algorithme peuvent bénéficier des apports de l’informatique quantique (cf. premier article de l’IA quantique). Il s’agit généralement d’inversion de matrices, de recherche d’extremum global, de calculs modulaires (à la base de la cryptographie), etc. Au-delà de savoir si la quantique peut ou ne peut pas accélérer certains traitements, ce découpage des codes permet surtout de réduire la facture cloud en limitant l’utilisation de VM quantiques au strict minimum (car leur coût horaire fera probablement grincer des dents).
Digression – Un exemple d’algorithme classique partiellement converti en quantique
Dans le cadre du DBN (réseau de croyance profonde), on peut isoler les étapes de pré-entraînement non supervisé des empilements de RBM et la phase de “fine-tuning” (ajustement fin). En effet, certains chercheurs se sont intéressés à une accélération quantique des étapes d’échantillonnage dans le cas d’un réseau convolutif de croyance profonde (oui, le nom est assez barbare). Le but étant de comparer la performance de l’échantillonnage quantique comparativement à des modèles classiques tels que l’algorithme CD (‘contrastive divergence’). Cette étude montre que la quantique permet de booster la phase de pré-entraînement, mais pas la phase de discrimination ! D’où l’importance de bien décomposer les étapes de l’algorithme, pour éviter de solliciter inutilement une machine quantique sur des calculs classiques longs et non transposables quantiquement parlant.
D’ailleurs, au-delà de l’optimisation tarifaire, le fractionnement des codes en niveaux d’abstraction est aussi et surtout une méthodologie essentielle dans la rédaction des scripts. Un article intéressant sur ce sujet qui montre que la gestion de l’abstraction (consistant à distinguer le “quoi” du “comment”) est une bonne pratique de développement qui en englobe beaucoup d’autres.
Étape 2 – Intégration aux dépôts et outils de CI/CD
Maintenant que les codes (et autres artefacts) du pipeline général sont judicieusement fractionnés par niveaux d’abstraction, il convient de les centraliser dans le dépôt. Cette démarche s’accompagne habituellement d’une standardisation des codes. Le but est de pour pouvoir les réutiliser facilement dans des contextes différents.
Le caractère générique et répétable d’un code peut s’obtenir au moyen d’une double “variabilisation”. La première est une généralisation intuitive du code en créant des variables relatives aux traitements des données (via des classes, méthodes, fonctions…). La seconde est la création de variables d’environnement, c’est-à-dire que le paramétrage du code s’effectue dynamiquement en fonction de l’environnement (au sens infrastructure) dans lequel il s’exécute. Par exemple, la variable “mot_de_passe” peut comporter plusieurs valeurs, chacune d’elles étant liée à un cluster spécifique.
Quant à l’automatisation des tests et du déploiement de ces scripts, la solution de DataOps peut soit intégrer des fonctionnalités de CI/CD, soit se connecter aux outils existants tels que Maven, Gradle, SBT, Jenkins/JenkinsX, etc. Ces derniers viennent récupérer les binaires centralisés dans le dépôt pour les intégrer dans le pipeline de traitement. Les codes deviennent alors des “jobs” qui s’exécuteront dans des clusters dédiés. Le pipeline doit enfin pouvoir historiser les versions des scripts et jobs qui le composent pour conserver une trace de toutes les livraisons précédentes et éventuellement procéder à des “rollbacks”.
Étape 3 – Virtualisation des données
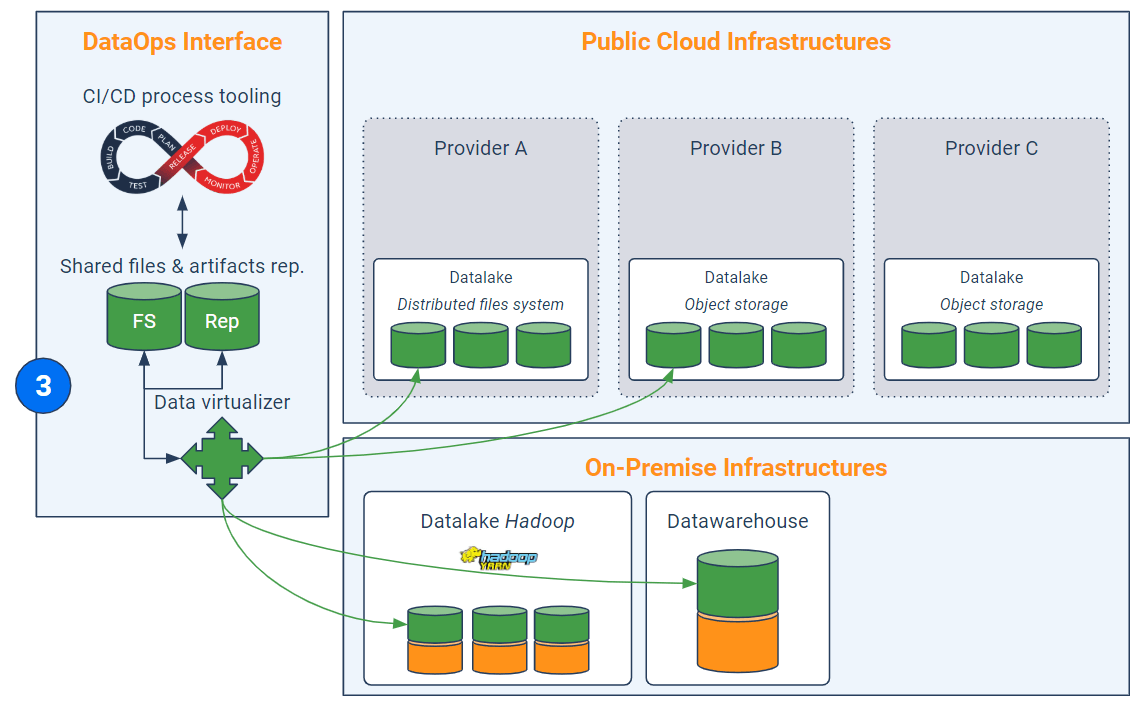
Avant-dernière étape, l’abstraction du stockage. En effet, dans la mesure où la finalité est d’exploiter des infrastructures éparpillées – ce qui demande déjà un énorme effort de programmation pour rendre les codes génériques – il est préférable de ne pas devoir tenir compte de la localisation exacte des données ni de devoir les répliquer à chaque traitement.
C’est typiquement le rôle d’un virtualisateur de données qui permet, généralement via des requêtes SQL ou REST, une connexion implicite à des sources de stockage intrinsèquement différentes en évitant le déplacement ou la recopie futile des données. Par ailleurs, les solutions de virtualisation des données apportent de fait un avantage concurrentiel indéniable dans la mise en oeuvre d’une gouvernance des données cross-infrastructures. J’entends par là la mise en oeuvre d’un référentiel transverse et unique avec gestion des métadonnées et des habilitations.
Le virtualisateur de données intervient au moment de la lecture des données (pour effectuer les traitements) et également en bout de chaîne pour écrire les résultats intermédiaires ou finaux dans une base (ou un cluster) locale ou distante.
Étape 4 – Répartition avancée de la charge
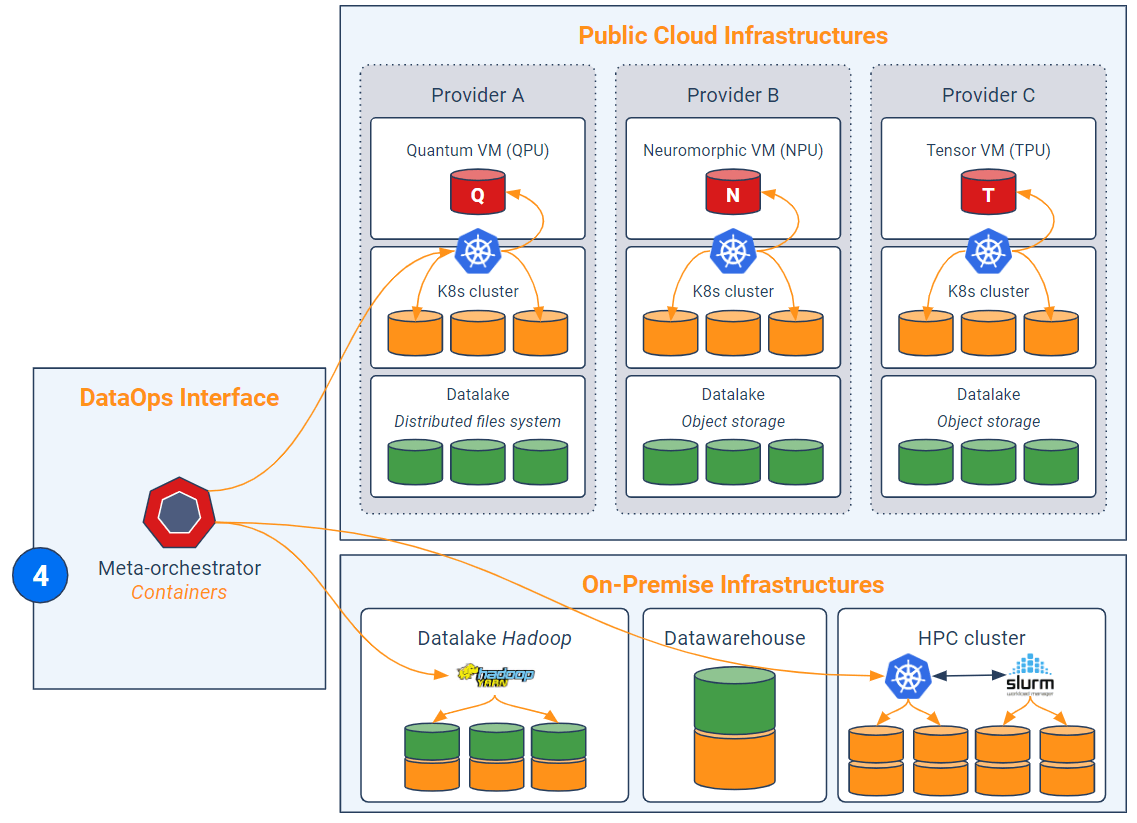
Maintenant que toutes les données sont mises à disposition (via le virtualisateur) et que les codes sont standardisés et découpés en unités fonctionnelles cohérentes, l’idée est d’orchestrer les traitements associés au sein du supercluster. Autrement dit, on cherche à exécuter les conteneurs algorithmiques dans les clusters appropriés.
Chaque cluster est gouverné par une solution jouant le rôle de planificateur/répartiteur de tâches et gestionnaire de conteneurs et de ressources physiques (ex : Yarn, Marathon, mais surtout Kubernetes). Aujourd’hui, tous les fournisseurs de cloud proposent des offres de type Kubernetes-as-a-service dans leurs clusters virtuels. La solution de DataOps doit aller un cran plus loin et jouer le rôle de “méta-orchestrateur”. Ce dernier vise à répartir les jobs parmi les orchestrateurs (Kubernetes) sous-jacents de chaque cluster. Le méta-orchestrateur est donc une couche d’abstraction additionnelle à Kubernetes. Lorsqu’une accélération quantique est nécessaire, le méta-orchestrateur est chargé de rediriger le conteneur algorithmique vers l’un des Kubernetes orchestrant les VM quantiques. Ainsi, le méta-orchestrateur s’assure du fait que seuls les jobs pertinents sont routés vers les VM quantiques, tandis que les autres peuvent s’exécuter on-premise ou sur des clusters clouds composés de VMs traditionnelles.
Quant aux problématiques de clusters HPC, il faut espérer la poursuite des développements d’interfaces entre Kubernetes et les ordonnanceurs de tâches sur grilles informatiques (ex : Slurm, IBM Spectrum LSF). Auquel cas, le méta-orchestrateur passera soit par Kubernetes (dans l’idéal), soit par l’ordonnanceur de grille HPC pour répartir sa charge.
En synthèse, l’essor des machines quantiques dans le cloud incitera les entreprises à optimiser la manière dont elles orchestrent leurs environnements analytiques et hybrides. Il s’agit avant tout d’une logique de souveraineté des données, de dépendance à des fournisseurs et de coûts (les calculs quantiques seront probablement très onéreux). L’interface DataOps, qui peut être une solution logicielle unifiée, est en particulier composée de quatre éléments : un outillage de CI/CD, un dépôt de fichiers partagés et de scripts, un virtualisateur de données et un méta-orchestrateur (en pratique, il faut aussi y adjoindre un dispositif de sécurité et un système de supervision globale). L’intérêt est triple : simplifier la gestion de données décentralisées, automatiser le déploiement de pipelines complexes et orchestrer le routage de certains codes lourds (compatibles au formalisme quantique) vers des clusters Kubernetes dotés de VM quantiques. Les entreprises seraient ainsi en mesure de gouverner leurs données en mode hybride, d’optimiser la répartition de charge et de contrôler leurs coûts (en particulier la facture cloud) en sollicitant les bons clusters au bon moment, en particulier lorsqu’il s’agit d’utiliser des serveurs HPC (ex : GPU, TPU, NPU, QPU, etc.).

Axel Augey est diplômé de l’Ecole Centrale de Lyon et de l’ESSEC. Il intègre notamment Saagie en 2017 en tant que Responsable du Marketing Produit puis occupe depuis 2020 le poste de Responsable Data chez papernest, start-up française spécialisée dans la simplification des démarches administratives et contractuelles liées au logement.